Tutorial 5, terrain callback
In the previous tutorial we looked at the terrain mesh, and discovered how it allows us to create a completely arbitrary surface composed of triangles that are typically used to create a terrain. One of the limitations of this, however, is that as the complexity of the terrain grows, Tokamak will begin to slow down when it is performing its collision detection.
The reason for this is that it has to check each rigid body in your scene against every single triangle in the terrain mesh. As the numbers of rigid bodies and of triangles in your terrain increase, this can quickly lead to situations where the physics becomes unworkably slow.
One possible way to avoid this would be to divide your terrain up into
sections and repeatedly call the SetTerrainMesh() function each
time the focus of your scene moves from one region of the map to another.
There are two drawbacks to this, however: firstly it limits all of your
physics processing to a single section of the game world, and secondly it
gives rise to the possibility of a performance hit in Tokamak each time you
set a new mesh.
To work around these problem, Tokamak provides an alternative way for you to tell it about the triangles that form your terrain. Instead of giving the entire terrain to the engine, it will call a function in your code every time it updates the position of each rigid body. Your function is responsible for returning a list of only the relevant triangles that the body might potentially be colliding with.
This has two major advantages over SetTerrainMesh(), as
follows:
1. As you have knowledge about how your terrain fits together, you are usually able to make a well judged calculation about exactly which triangles are relevant for collision detection. This can take advantage of binary space partitioning algorithms and can usually be easily reduced to just a handful of triangles (eight or less on a grid-based terrain).
2. It allows you to handle the collisions differently for each rigid
body. For example, some bodies may completely pass through the terrain by
not returning any triangles. Or you may have two sets of terrain, with some
bodies colliding with one set and some with the other. There are all sorts
of possibilities in this area that are simply not available using
SetTerrainMesh().
While the terrain callback may at first look a little daunting, it's actually not too complicated. Much of this code is based on that of tutorial 4, so if you've not read that yet then this is probably a good time to do so.
The only real difference during the setup of the rigid bodies is the
addition of this code in the loop that creates our spheres inside
InitPhysics():
// Set the index of the triangle into the UserData of the rigid body. // We can retrieve this in the Terrain callback in order to find // out which rigid body we're testing for. gSpheres[i]->SetUserData(i);
This gives a unique number (1, 2 or 3) to each of the bodies. We'll use this in the terrain callback to determine which sphere is being collision- checked. For the purposes of this code, we'll use this to highlight the relevant triangles in a different colour for each sphere.
The terrain mesh in this example is generated in exactly the same way as
in tutorial 4 (though the SetTerrainHeights() function returns
a much less random terrain this time -- essentially a bowl shape so that our
spheres roll around it). We still set up the neTriangleMesh
object, though this time it's a global variable as we'll refer to it in
several parts of the code.
Now, the BuildTerrainMesh() procedure no longer calls
SetTerrainMesh() once it has built the triangle mesh. It simply
returns back to InitPhysics. The extra magic line in
InitPhysics() that initialises the terrain triangle callback is
as follows:
gSim->SetTerrainTriangleQueryCallback(TerrainQueryCallback);
Once this has been executed, Tokamak knows that it needs to call the
function in your code called TerrainQueryCallback() every time
it is processing the position of a rigid body in order to get the list of
triangles it should test against for collisions.
So far so good, now we get to the callback function itself. The header of the function is shown here:
void TerrainQueryCallback(const neV3 & minBound, const neV3 & maxBound, // bounds of object to test s32 **candidateTriangles, // indices of triangles to be tested neTriangle **triangles, // all possible test triangles neV3 **vertices, // triangle vertices s32 *candidateCount, // number of candidate triangles s32 *triangleCount, // number of possible test triangles neRigidBody *rb) // body to test {
This looks a bit complicated at first, but really it's not too bad. Let's take a look at each parameter:
const neV3 & minBound, const neV3 & maxBoundThese two parameters pass two points into the function that form an "axis-aligned bounding box" (commonly abbreviated to AABB) which completely contains the rigid body. This essentially means that the lowest of all of the X, Y and Z coordinates are passed in the
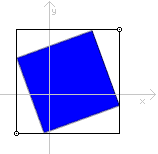
minBoundparameter, and the highest of all the coordinates are passed in themaxBoundparameter.If you can't visualise that, here's an example in 2d:
The black rectangle shows an axis-aligned bounding box around the blue rectangle. Even though the blue rectangle is not aligned to the X and Y axes, the AABB is. This allows the AABB to be described using just two 2D points -- one at the bottom/left (the minimum X and Y values across all vertices in the blue rectangle) and the other at the top/right (the maximum X and Y values).
The
minBoundandmaxBoundparameters provide exactly the same information but in 3d. The two points describe a cuboid that perfectly and completely contains the rigid body.s32 **candidateTrianglesProvides a pointer to a pointer to the indices of the triangles to test against.
Let's try that again in English, shall we?
When we return from the function we will provide a full list of triangles against which collision may be performed. However, we can tell Tokamak to ignore most of those triangles and instead get it to use just a subset of them. This parameter allows us to pass the indices of the triangles which are to be used for collision detection.
So if we return an array of 100 triangles but we only want triangles 10, 20, 30 and 40 to be used for collisions, we would return a pointer to an array containing the values
{10, 20, 30, 40}. This would result in only those four triangles being used for the collision test despite the fact that we returned the definitions of all 100, saving a lot of unnecessary processing.neTriangle **trianglesThis is where we actually return the details of the triangles described above. Again, we use this to return a pointer to an array of neTriangle objects.
As you'll know from the previous tutorial, each triangle details the indices of each vertex within a vertex array rather than storing the actual vertex positions, so we'll need to provide the vertex array too. Which brings us to...
neV3 **verticesA pointer into which we'll provide the address of an array of vertices. This array must encompass every vertex referenced by the
trianglesarray, and defines the actual position of each vertex in 3d space, just as in the previous tutorial.s32 *candidateCountA pointer to an integer value into which we place the number of candidate triangles that are present in the
candidateTrianglesarray above.s32 *triangleCountA pointer to an integer value into which we place the total number of triangles that are present in the
trianglesarray above.neRigidBody *rbA pointer to the rigid body that is being tested for collisions. We can use the body's User Data to retrieve more information about the body, as shown below.
Note: If your code doesn't want to work with this parameter, you may have an out-of-date version of the Tokamak SDK. The initial version of the v1.2 SDK did not include this parameter. An updated version was released shortly afterwards with the parameter restored -- download the latest version if this is causing problems.
So now we know what all the parameters are for, it's time to figure out what to do with them.
There are two ways in which you can use the terrain callback. The first
of these is to add all of the triangles that are to be tested to the
triangles array, omitting any that are not relevant for the
collision check. In this case, the candidateCount and
triangleCount will both contain the same value (the number of
triangles in the triangles array). The
candidateTriangles array will list all of the triangles (so
index zero of the array will contain the value zero, index one will contain
the value one, etc.).
The second way is to return the entire set of all possible triangles (the
entire terrain) in the triangles array, and inform Tokamak
which of them are relevant using the candidateTriangles array.
In this case the candidateCount will be the number of triangles
to be checked and the triangleCount will be the total number of
triangles in the terrain.
Both of these are valid approaches, and you'll need to decide which is more appropriate for your application. For our code we'll use the second approach. The reason for this is that we already have valid arrays of triangles and vertices in exactly the format Tokamak is expecting -- we built them for our triangle mesh earlier on. Because we pass back a pointer to an array, there's no bulk data copying to be done; we just return a pointer to the existing array.
That means that there's no work to do for the triangles or
vertices parameters, and we know the triangleCount
too. But we still need to work out the details for the candidate
triangles.
The first thing we do is declare the variables needed to do this, as follows:
static s32 sCandidateTriangles[TERRAIN_TRIANGLECOUNT]; int iCandidateIndex = 0; int i, j; neV3 minTri, maxTri; float fThisX, fThisY, fThisZ;
The sCandidateTriangles array is declared as
static. There are two important reasons for this: firstly, the
data will be used by Tokamak after the callback function has returned and
its variables have gone out-of-scope. Declaring the array as
static means that it will be retained in memory and the pointer
to its data will still be valid. The second reason is one of performance.
When the array is static, C++ will allocate memory for it at the beginning
of the application execution. That memory will stay valid until the
application terminates. A non-static array would need to be reallocated
every time the callback function is executed.
This leads us to an important point about the terrain callback: this
function will potentially be executed hundreds of times for every call to
Tokamak's Advance() method. For this reason you should be
extremely careful with the complexity and execution speed of code within it.
Performing slow operations here could cause your whole application to slow
down for no apparent reason. You should avoid memory allocations and should
try to avoid any unnecessary calculations too.
The next block of code in the function is as follows:
// Loop through each triangle in our terrain for (i=0; i<gTriMesh.triangleCount; i++) { // Set the min and max X and Z values to be the first point in the triangle fThisX = gTriMesh.vertices[gTriMesh.triangles[i].indices[0]].n.X; fThisY = gTriMesh.vertices[gTriMesh.triangles[i].indices[0]].n.Y; fThisZ = gTriMesh.vertices[gTriMesh.triangles[i].indices[0]].n.Z; minTri.Set(fThisX, fThisY, fThisZ); maxTri.Set(fThisX, fThisY, fThisZ); // Loop for the other two points in the triangle in order to find the // minimum and maximum coordinate values across all three vertices. for (j=1; j<3; j++) { fThisX = gTriMesh.vertices[gTriMesh.triangles[i].indices[j]].n.X; fThisY = gTriMesh.vertices[gTriMesh.triangles[i].indices[j]].n.Y; fThisZ = gTriMesh.vertices[gTriMesh.triangles[i].indices[j]].n.Z; if (fThisX < minTri.n.X) minTri.n.X = fThisX; if (fThisY < minTri.n.Y) minTri.n.Y = fThisY; if (fThisZ < minTri.n.Z) minTri.n.Z = fThisZ; if (fThisX > maxTri.n.X) maxTri.n.X = fThisX; if (fThisY > maxTri.n.Y) maxTri.n.Y = fThisY; if (fThisZ > maxTri.n.Z) maxTri.n.Z = fThisZ; }
In this first part of the loop we're trying to find the minimum and maximum values on the X, Y and Z axes -- essentially the AABB of each triangle. As we are using a static terrain mesh we could (and should) precalculate all of this, saving a lot of processor time within the callback. In fact you'll find that if you increase the size of the terrain up to just 25x25 or 35x35 quads, the performance will begin to severely degrade. Precalculating all of these triangle AABBs would resolve the problem. For the sake of clarity I've left the code as above.
Once we know the AABB of the triangle, we can use the AABB of the rigid body to determine whether the rigid body potentially intersects the triangle. This is done by seeing whether the minimum position of the rigid body in each axis is less than the maximum position of the triangle, and also the maximum position of the rigid body is greater than the minimum position of the triangle. If these conditions are all true across all three axes, the rigid body and the triangle potentially intersect. This means that the triangle should be included within the collision detection.
// Now we know the bounds of the triangle, do the bounds of the // rigid body fall within them? if (minBound.n.X <= maxTri.n.X && maxBound.n.X >= minTri.n.X && minBound.n.Y <= maxTri.n.Y && maxBound.n.Y >= minTri.n.Y && minBound.n.Z <= maxTri.n.Z && maxBound.n.Z >= minTri.n.Z) { // Yes, the rigid body is vertically in line with this triangle. // Add this triangle to the array of candidate triangles. sCandidateTriangles[iCandidateIndex] = i; iCandidateIndex += 1; // Use the GetUserData method to retrieve the sphere index // we previously placed into the rigid body. We'll use this // as part of a binary shift so that each rigid body sets // a corresponding bit in the giTriangleActive array. giTriangleActive[i] |= 1 << rb->GetUserData(); } }
When this occurs we add a new item to the
sCandidateTriangles array and increment the array index pointer
(which also serves as a count for the number of items added to the array).
We also set a value into the giTriangleActive array. This is a
global array used purely to provide visual feedback in the rendering loop
about which triangles are actually being included in the collision check. We
retrieve the User Data value that was placed into the rigid body during the
InitPhysics() function and use it to set up a bit-mask in the
array.
Note that you can pass any unsigned integer into the User Data value of the rigid body. This could be a pointer to a class or a data structure. If you are wrapping your rigid bodies inside C++ classes, you can place a pointer to the wrapper object inside each rigid body's User Data. This allows you to easily retrieve the object data during the collision check (which could then be used to control exactly how the check is performed).
When this loop completes, we actually have everything we need to pass back to Tokamak. The final piece of code here sets all the values and array addresses into the pointers that Tokamak has passed us:
// Now we've built the array of candidate triangles, // we return values back to Tokamak as follows: *candidateTriangles = sCandidateTriangles; *triangles = gTriMesh.triangles; *vertices = gTriMesh.vertices; *candidateCount = iCandidateIndex; *triangleCount = gTriMesh.triangleCount;
candidateTriangles is given a pointer to the static array of
triangles we've constructed. triangles and
vertices are both pointed to the pre-constructed arrays that we
put into the triangle mesh during the call to InitPhysics().
candidateCount is loaded with the number of triangles we added
to the candidateTriangles array, and triangleCount
gets the total number of triangles in the triangle mesh.
The last major change to the code in this project is in the
Render() function. In order to draw the candidate triangles to
make the process clearer, I've modified the rendering of the terrain to draw
each triangle individually. For each one it checks to see whether the
triangle was involved with any collision check, and sets the ambient
lighting to include full red, green or blue depending on which of the
spheres was involved. This leads to a terribly inefficient piece of
rendering code, but I've written it this way because it's easy to read.
// Set the vertex and index stream for the terrain gD3DDevice->SetStreamSource(0,vbFloor,sizeof(strVertex)); gD3DDevice->SetIndices(ibFloor, 0); // Reset the view matrix to the identity matrix dxLoadIdentity(); dxApplyMatrix(gD3DDevice); // Draw the terrain for (i=0; i<TERRAIN_TRIANGLECOUNT; i++) { // Assume the ambient light will be the "normal" colour iFloorColour = 0x00202020; // Set the red, green or blue components of the ambient // light to full strength if one of our spheres is over // this triangle so that we can highlight it. if (giTriangleActive[i] & 1) iFloorColour |= 0x00ff0000; if (giTriangleActive[i] & 2) iFloorColour |= 0x0000ff00; if (giTriangleActive[i] & 4) iFloorColour |= 0x000000ff; // Set the ambient light so that this floor triangle is rendered // in the colour we've defined gD3DDevice->SetRenderState(D3DRS_AMBIENT,iFloorColour); // Set the vertex and index stream for the terrain gD3DDevice->SetStreamSource(0,vbFloor,sizeof(strVertex)); gD3DDevice->SetIndices(ibFloor, 0); // Draw this triangle gD3DDevice->DrawIndexedPrimitive(D3DPT_TRIANGLELIST, 0, TERRAIN_VERTEXCOUNT, i*3, 1); } // Reset ambient lighting for subsequent rendering gD3DDevice->SetRenderState(D3DRS_AMBIENT,0x00202020);
When you run the project, you will notice that the spheres roll perfectly
normally, just as they would have done using the
SetTerrainMesh() call in the previous tutorial. The important
thing to note however is that only the triangles that light up in different
colours as the spheres roll around are actually being checked for
collisions. All other terrain triangles are completely ignored.
It's also worth noting that when a rigid body "sleeps" (Tokamak stops updating its position because it considers that body as stationary), the coloured triangles under that sphere suddenly vanish. This is not a bug, but one of the many optimisations in Tokamak that help to maintain its exceptional performance. As soon as the body is sleeping, Tokamak stops performing any collision checks against the terrain until another rigid body (or the application of a force upon the body from within your program code) wakes it up again.
That concludes this tutorial. The source code and a compiled executable for this tutorial are available in the following .zip file.
TokamakTutorial5.zip
| << Tutorial 4, terrain mesh << |
If you have any comments or suggestions regarding this article, please don't hesitate to contact me.
This article is copyright © Adam Dawes, 2004.
It may not be copied or redistributed without my express written permission.